1. Introduction

Shell structures are a group of objects that are subject to periodic shape control required both for the safety of the self-supporting structure and for functionality purposes. Displacement control may apply either to selected points of the structure or the entire shell, especially with the use of laser scanning technology. The point cloud from the current measurement can be compared directly with the point cloud from the previous measurement. It is the simplest method that determines the distances between the closest neighbouring points (Javaheri et al., 2020; Vanneschi et al., 2017). The distances are not calculated along the normals to the model surface because it is not being determined; so, in the case of low resolution of point clouds, significant method errors can occur. Better accuracy is possible when comparing the point cloud with a mesh (Antova, 2019; Neuner et al., 2016; Park and Lee, 2019) created based on the second point cloud. The mesh model allows to determine the normals at any point, so the resolution of the point cloud no longer determines the accuracy of the comparisons. However, such a model consists of flat triangles, which may cause some distortions when describing the curvilinear structure of the shells. The solution is to use spline functions (Farin and Farin, 2002; Piegl and Tiller, 2012), which allow to create a model with a continuous curvature. However, in the case of structures with edges, the continuous curvature causes undulations of the function, so these types of models can also be distorted.

Problems related to the accuracy of the direct comparison of point clouds induce the search for the methods of local modelling of the immediate vicinity of the point (Jafari, 2016; Urbach et al., 2020). However, better results are achieved by creating a global model that takes into account local irregularities. The aforementioned triangle meshes are such a model. They can be determined in many ways and significantly differ from each other (Botsch et al., 2010; Remondino, 2003; Wongwaen et al., 2012). Most of the methods aim at building meshes using Delaunay triangulation (Boissonnat and Cazals, 2002; De Loera et al., 2010), which allows to construct triangles whose shapes are the most similar to equilateral ones. In the simplest case, the measured points are the vertices of the triangles. In practice, with dense point clouds, this approach is ineffective. Most frequently, at the stage of noise reduction in point clouds, new vertices are determined by approximation, with a more rare distribution than cloud points. Triangles with larger surface areas contribute to the increased distortion of modelling curvilinear objects. If these objects have edges, their chamfering may appear in the form of triangles determined transversely to the edges (Attene et al., 2013). In addition to the most popular cloud-to-cloud or cloud-to-mesh comparisons of periodic measurements, more complex curvilinear spline surfaces (Non-Uniform Rational B-Spline, NURBS) can be used. Currently, they exist in several approximation varieties. The simplest one creates a surface directly based on points (Brujic et al., 2011; Kiciak, 2019). Modelling of more complex structures requires the initial creation of a mesh, determining the approximate surface geometry based on this mesh and the construction of the proper spline surface (Wang et al., 2011; Zhang et al., 2002). The creation of the most complex shapes requires additional outlining of the areas on the mesh, inside which surface patches with independent parametrisation are determined (Lin et al., 2007; Zhang et al., 2011). The spline surfaces are fitted into the point cloud using the least-squares method, and each segment is created based on a certain group of points, the number of which depends on the accuracy of fitting. Similar to meshes, these surfaces do not pass exactly through the points; but thanks to the continuity of the curvature, they can correctly approximate the shape of shell structures. However, the accuracy of the edge approximation remains a problem. They are not flattened as in mesh models, but undulations occur around them because spline functions cannot approximate those shapes that do not have curvature continuity with good accuracy.

Periodic measurements can be compared by building a model for one measurement and comparing the point cloud from the second measurement to it, or by constructing models for both measurements. Due to the fact that model creation is accompanied by approximation errors, the comparison of the two models will contain a double approximation error.

2. Research objective related to the use of spline functions

The research was aimed at verifying the accuracy of determining the displacements of a shell structure using the following comparisons: cloud to cloud, cloud to mesh and cloud to spline surface. The structure consisted of several independent patches separated by edges. It also had several smaller edges in its structure, affecting the modelling accuracy. The inspection of the structure during periodic surveys revealed two local deformations of the surface, related to the deformation of the sheet metal covering. The correct displacement determination process should indicate the actual periodic shape changes (deformations) and, at the same time, avoid the apparent changes (pseudo-deformations) caused by surface modelling errors.

It was essential to compare the displacements determined by spline functions with the other methods in this study. The theoretical properties of splines, on the one hand, encourage their use for smooth surface patches and, on the other hand, indicate potential distortions for edges. The spline functions are determined using the Bernoulli–Euler equation, which provides a mathematical description of a bending bar in terms of elasticity (Kiciak, 2019):

Therefore, they have continuity of the function and its first two derivatives (curvature continuity). It is fulfilled within patches of the surface, but at sharp edges, it causes undulations of the function. This is a serious problem when approximating shapes represented by relatively sparse point clouds (e.g. acquired with total station instruments). In the case of laser scanning, the density of points is high and many more segments of the spline function are determined; this has a direct impact on the reduction of undulations. The equation describing the convergence of the spline function S to the approximated function f (Kiciak, 2019) depends on the parameter h, which is given by the distance between successive points:

Decreasing the distance h, therefore, reduces the value of the approximation error at a quadratic rate. As the density of the point cloud increases, the scale of errors resulting from the description of edges by spline functions decrease rapidly. It is important to check that this scale will be small enough to avoid pseudo-deformation when creating the surface. This is difficult to determine theoretically because in practice, the number of spline segments does not follow directly from the number of measured points. This is because spline surfaces are created by least-squares approximation, which can arbitrarily decide how many neighbouring points create a single segment of a spline function. Approximating B-spline surfaces are used to create surface patches:

Depending on the magnitude of the approximation error, the number of points forming adjacent spline segments will change in the process of iterated solution correction. Usually, the desired approximation accuracy can be set a priori, but this is often unreliable for complex surfaces. The accuracy of the process is estimated after the last iteration.

Some of the problems with errors along the edges can be removed by creating separate surfaces along the main edges. This is relatively simple if the object contains clear edges separating large surface patches. If these are edges resulting from cracks, ribs or various small pieces of technical infrastructure, their precise separation from the point cloud and subsequent modelling with separate spline patches become problematic.

A comparative study with other methods of determining displacements between point clouds will make it possible to determine the suitability of models using the spline functions for this type of task.

3. Test procedure

The research object was subjected to periodic surveys using laser scanning: the first one was performed in 2013 (Figure 1a), and the second one in 2020 (Figure 1b). Both measurements were performed with the Leica C10 scanner with a position of point accuracy of 6 mm and a precision of 2 mm. The primary measurement was carried out from seven stations, which were registered into one point cloud in the Leica Cyclone software using HDS 6″ targets. The mean transformation error was 4 mm. The current measurement was carried out from 10 stations using the cloud-to-cloud merging method, and the average process error was 6 mm. The observed surface deformations occurred on both sides of the front shell patches. In 2013, the surface had a deformed end segment of the flange extending along the frontal patch (Figure 2a). In 2020, the flange had already been repaired (Figure 2b), but one of the tiles had been damaged (Figure 2d) compared to the original measurement (Figure 2c). The deformations were small and reached values of about 30–40 mm. In their vicinity, there were surface elements with edges (the flange itself, approximately 40 mm high) and longitudinal slats, approximately 30 mm high. These elements could distort modelled surfaces and be misinterpreted as pseudo-deformations of the structure.

Figure 1

The shell studied during the measurements performed in 2013 (a) and 2020 (b)

Figure 2

The flange torn off and bent in 2013 (a) and repaired in 2020 (b). The tile damaged in 2020 (d) compared to 2013 (c). The photos show the edges of the flange and narrow longitudinal slats forming additional edges

The current measurement from 2020 was used as the base one, which the primary measurement from 2013 was compared to. This was due to the higher average resolution of the current measurement (8 mm compared to 14 mm of the primary model) and better coverage of the structure with points (Figure 3). Both point clouds had a gap in the upper part of the frontal patch due to the lack of the visibility; in addition, the primary point cloud had gaps due to obstructions by branches and the chimney.

Figure 3

Point clouds from the epoch 2013 (a) and 2020 (b)

The periodic measurements were transformed into a common coordinate system in the Leica Cyclone software by the cloud-to-cloud method using 20 fit points selected at the corners of the tiles covering the structure. The average accuracy of the process was 3 mm.

The current measurement mesh model was created in Solid-works with the lowest level of smoothing applied. Nevertheless, the chamfering of the edges is visible (Figure 4a). The spline model was created in Rhinoresurf. Considering the surface undulations formed at the places of curvature discontinuity, the point cloud was separated along the main edges of the patches and each of them was modelled separately. The edge elements, that is, the flange and slats, were not separated from the patches. This resulted in undulations of the spline surfaces along their edges (Figure 4b).

Figure 4

Chamfering of the mesh edge (a), undulations of the spline surface along the edge (b)

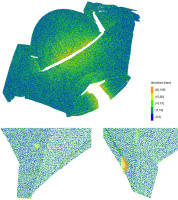
The models prepared in this way were then used to determine the displacements in relation to the point cloud from the primary measurement. Comparisons by cloud-to-cloud and cloud-to-mesh methods were performed in CloudCompare and by cloud-to-spline surface in Rhinoceros. The result of the direct comparison of point clouds is illustrated in Figure 5. The periodic displacements of the structure determined by comparing the point cloud with the mesh model are demonstrated in Figure 6 and with the spline model in Figure 7.

Figure 5

Periodic displacements of the structure determined by direct comparison of point clouds. View of the entire structure as well as the left and right parts of the front patches with deformations and edges

Figure 6

Periodic displacements of the structure determined by comparing the primary point cloud with the mesh model created for the current measurement. View of the entire structure as well as the left and right parts of the front patches with deformations and edges

Figure 7

Periodic displacements of the structure determined by comparing the primary point cloud with the spline model created for the current measurement. View of the entire structure as well as the left and right parts of the front patches with deformations and edges

4. Analysis of results

As a result of the performed research studies, two similar images of periodic deformations were obtained by using the mesh and spline models and an image of deformation different from these two was obtained, which was determined by a direct cloud-to-cloud comparison. In order to systematise the deviations seen in Figures 4 and 5, Table 1 has been presented, containing the percentages of the individual deviation ranges and the average deviations.

The mean deviation of the primary point cloud from the current spline model was the smallest and amounted to 1.9 mm. The mean cloud-to-mesh deviation was 2.8 mm, while the cloud-to-cloud deviation increased to 7.1 mm. A significant mean deviation of the cloud-to-cloud comparison resulted from the limitations of this method, conditioned by the resolution of the point cloud. There was a visible increase in the value of deviations (pseudo-deformations) from the bottom to the top of the structure (Figure 5). The upper parts of the structure were measured at increasingly sharper angles due to the curvature of the surface, which resulted in a dilution of observation (Figure 7). As a result, as the height increased, it became more and more difficult to find close proximity to the points in clouds from periodic measurements. The pseudo-deformations determined between the point clouds in the upper parts of the structure exceeded the value of 15 mm, and in the flattest places, even 20 mm. In the lower parts of the structure, where the scanning resolution was higher, most of the deviations fell within the range of [0, 5] mm; however, the entire structure was densely covered with random deviations of about 5–15 mm. The real periodic deformations of the structure were correctly determined. In the lower left part, a protruding tile was visible, and in the right, a deformed tip of the flange. A narrow band of pseudo-deformations appeared along the rear part of the flange, which was related to the smaller point coverage of its vertical part (Figure 3).

Comparison of the primary point cloud with the mesh model of the current measurement gave a significantly different image of the deformation (Figure 5). The use of a continuous model eliminated the deviations in the upper, flattened parts of the surface because the displacements were determined along the normal to the surface. There were no random deviations scattered across the surface, either. However, there were deviations, mainly within the range of [5, 10) mm, corresponding to the convex edges of the tiles covering the surface. There were no real deformations in these places, and the convex edges were chamfered by transverse triangles generating pseudo-deformations of small values. The actual surface deformations were correctly identified – the protruding tile on the left and the bent end of the flange on the right. Pseudo-deformations along the back part of the flange were marked on a larger scale than the cloud-to-cloud comparison. It was caused by the edge chamfering illustrated in Figure 3a. Pseudo-deformations related to chamfering also occurred along the narrow slats illustrated in Figure 2. Deviations related to the occurrence of pseudo-deformations reached values comparable to real deformations, and without photographic documentation, it would be difficult to indicate the real deformations. The mesh model additionally allowed to show the difference between the measurements resulting from leaf deposits along the concave right edge. They are visible as groups of deviations in the range 5–20 mm. During the cloud-to-cloud comparisons, these deviations were invisible due to method errors.

Comparison of the primary point cloud with the spline model of the current measurement (Figure 7) revealed the smallest global differences between periodic measurements, which is consistent with the photographic documentation of the structure. Random deviations were formed over the entire surface, but in a smaller number and scale than for the mesh model. The deformations associated with the cracked tile on the left were visible, but their size was smaller than for the other comparisons and smaller than in reality (Figure 2). However, the deformation of the flange end was correctly determined. It resulted from the properties of the spline surface and the measurement epoch for which the spline surface was constructed. The tile crack was observed in the actual measurement for which the model was constructed. The spline surface could not describe elements with discontinuous curvature well, in particular, displacement-related cracks. This place was smoothed out by a continuous curvature surface. The comparison of such a model with the primary point cloud showed deformations smaller than the real ones. The deformation of the end of the flange was correctly determined because the spline surface modelled the already repaired flange without cracking or detachment. In this case, there were no deformations of the spline model. Similar to the mesh model, it was possible to determine the differences in measurements associated with the deposition of leaves along the concave right edge. There were also pseudo-deformations along the back part of the flange and along the slats. The pseudo-deformations had values greater than the actual deformation associated with the tile cracking. Therefore, also in this case, without photographic documentation, it would be impossible to indicate the actual deformations correctly.

On comparing the percentages of deviations for individual methods (Table 1), it can be seen that the worst results were obtained for the cloud-to-cloud method. The compliance of the results from the measuring epochs in the interval (0, 5] mm was obtained only for about 38% of the points, while for the other methods, it was about 95–99%. Some of the larger deviations for all methods are due to actual deformations of the object. The cloud-to-mesh method differs from the cloud-to-spline method mainly in the increase of deviations in the intervals (5, 10] mm and (10, 15] mm. This is a total increase from about 1% to about 4.4%. These deviations appeared mainly at the convex edges of the tiles, which were chamfered by the mesh triangles.

5. Conclusions

The conducted research allowed to identify the advantages and disadvantages of individual methods of comparing periodic measurements for shell structures with edges. It was not possible to indicate a single universal method of determining deformations because the description of smooth, curvilinear patches required other tools than the edge description. The worst global results were obtained for a direct cloud-to-cloud comparison. This was due to method errors, conditioned by the resolution of the point cloud, which was variable for a structure with a curvilinear surface. However, locally, for a dense point cloud, the actual deformations were determined correctly and pseudo-deformations occurred to a small extent. Periodic comparisons based on surface models eliminated global comparison errors because deformations could be determined in the direction normal to the continuous model surfaces. Unfortunately, due to approximation errors, the modelling contributed to the formation of pseudo-deformations along the edges of the structure. For meshes, they resulted from the chamfering of the edges, and for the spline surfaces, they resulted from the undulations along the edges. Modelling of the surface of the patches gave better results of periodical comparisons for spline models than for mesh models. The situation changed for the local deformations in the form of a crack that was smoothed by the spline model. Ultimately, each of the periodic displacement determination methods proved to be useful within a certain range of applicability. The best effects of detecting real deformations and suppressing pseudo-deformations would be achieved by combining the cloud-to-cloud and cloud-to-spline surface methods, while the cloud-to-mesh comparison seems to be the single most universal method.