Gauss-Markov model with random parameters to adjust results of surveys of geodetic control networks

Marek Banaś; Józef Czaja; Janusz Dąbrowski

doi:10.2478/rgg-2021-0001

1. Introduction

Alignment of an engineering object project in the field is performed with reference to the points of the geodetic control network which have been previously determined. The coordinates of the geodetic control network points are determined on the basis of the results of surveys of the geodetic control network elements and with connection to the national spatial reference system. Electronic tacheometers, precision levels and Global Navigation Satellite Systems (GNSS) techniques are used to observe these elements. The accuracy of the survey of geodetic control network elements is much higher than the accuracy of determining the coordinates of the reference points.

In order to adjust the results of the survey of geodetic control networks connected to the national spatial reference system, the Gauss-Markov (G-M) model is applied most frequently, including the weighting matrix for the observed values and the apparent observation equations (pseudo-observations) for the coordinates of the reference points. For the pseudo-observations, the respective weights resulting from the accuracy of the analysed point coordinates are determined as well. In this case, numerous authors of scientific papers use sequential adjustment of survey results, that is, adjustment conducted in several steps.

The issues related to the selection of respective weights to adjust the survey results in geodetic point networks have been the subject of many scientific papers. The ones discussed by the authors: Baarda (1968); Rao (1982); Teunissen (2000), and Cross (1985) are the most compatible with the considerations included in this paper. One of the methods of the geodetic network optimisation is the strategy aiming at adjusting the accuracy of observation, which was developed by Kampmann (1994) and Caspary (1998). Another proposal for selecting observations and their weights was presented by Hekimoglu (1998) and Kampmann and Krause (1996). The issue of selecting respective weights when determining the coordinates of geodetic points is strictly related to the internal and external network reliability. The theory of network reliability is the subject of several scientific papers, and the precursors of these studies are Baarda et al. (1967); Baarda (1968, 1977) and Pope (1976). The papers of Prószyński (1997, 2000) constitute significant achievements in this field. The issues related to the design of optimal geodetic control networks and their connection to the national spatial reference system are solved in Dąbrowski (2014).

The coordinates of the points of the national spatial reference system are determined on the basis of previous surveys and they are specified with the appropriate accuracy, which is included in their covariance matrix. The coordinates of the geodetic control network points are determined more accurately than the coordinates of the points of the national spatial reference system and due to this, the results of the surveys of the geodetic control network have to be adequately incorporated into the coordinates of the reference points. In order to conduct this incorporation, it may be assumed that the coordinates of the reference points are random, that is, they have a covariance matrix, which should be used in the process of adjusting the results of the geodetic control network observation. This research paper presents the principles for the estimation of the Gauss-Markov model parameters applied in case of those geodetic control networks in which the coordinates of the reference points have random character, that is, they will have a covariance matrix. The verification of these estimation principles has been illustrated by the example of a fragment of a levelling geodetic control network, which, with regard to elevation, is connected to two points of the national spatial reference system.

2. Theoretical principles of Gauss-Markov model (L, AX, H) with random parameters

For determining the coordinates of geodetic network points constituting geodetic control, the following may be observed: horizontal and vertical angles, horizontal and spatial lengths, coordinates of 3D points in the established reference system as well as elevation differences of the selected points. For each observed value of λ, an observation equation in the general form may be formulated:

(1)

δλ+d(λ)=λobs−λapp

where:

δ_λ – represents a random error to the observed value λ_obs,
d(λ) – represents a differential of the function describing the variability of the analysed element λ, relative to the coordinates of the geodetic network points that define this element,
λ_app – is an approximate value of the analysed element determined on the basis of approximate values of the coordinates of geodetic network points.

Let L, with the size of n × 1, be the vector of random variables constituting the differences between the observed values of geodetic point network elements and their approximate values, that is (λ_obs − λ_app). The average value of this vector may be described with the use of fixed linear models AX, where X (u × 1) is a vector of unknown parameters (corrections to the approximate point coordinates) while A (n × u) represents the matrix of coefficients defined with the use of values of partial derivatives occurring in the differentials d(λ). It is assumed that for the selected unknowns (x₁, x₂, …, x_i) of the vector X, it is possible to define a priori the covariance matrix [Cov(x₁, x₂, …, x_i)]⁻¹. When completed with zeros to the square matrix of the (u × u) size, it represents the covariance matrix C_X. The inverse matrix Cov(x₁, x₂, …, x_i)⁻¹ completed with zeros to the square matrix of the (u × u) size, will be represented by the matrix CX−1 . Let the matrix H (n × n), whose inverse corresponds to the weighing matrix P, be the matrix of observation covariance L with fixed X, that is,

(2)

H=V(L/X).

Based on the above-mentioned assumptions, the matrix of conditional covariances of the observation vector L may be defined as follows:

(3)

V(L)=E[V(L/X)]+V[E(L/X)]=H+V(AX)=H+ACXAT.

Estimation of the average value of the vector L will be conducted with the use of estimators of parameters representing vector X, the covariance matrix (3) and the method of least squares. For this purpose, the square form F for random deviations will be written, but with regard to the matrix of conditional covariances of the observation vector L, for which the minimum relative to the vector of unknowns X will be sought, that is,

(4)

F=[(L−AX)T(H+ACXAT)−1(L−AX)]=min.

The condition necessary for the minimum of the function (4) may be written in the following symbolic form:

(5)

∂F∂X=0.

Having conducted differentiation of the function (4) and after further matrix transformations, an equation system is obtained and it complies with the condition (5), that is,

(6)

(CX−1+ATH−1A)⋅X^=ATH−1⋅L.

On the basis of the dependence (6), with regard to the relationship H⁻¹ = P, the final formula for calculating the estimator of the vector X^ is derived in the following form:

(7)

X^=(CX−1+ATPA)−1ATP⋅L.

In order to examine the effectiveness of this estimator, it is necessary to conduct full analysis of the variance with interval estimation. The vector of random deviations δ to the estimated linear model AX^ is the difference between the vector L and its average value E(L)=AX^ , that is,

(8)

δ=L−AX^.

The variance for the estimated model, resulting from the mutual incompatibility of the results of the observations of the geodetic control network, is defined by exemplar:

(9)

σ^02=δTp−1δn−u,

where n is the number of the observed elements, and u = rank (A).

The covariance matrix of the estimated vector of the parameters X^ is determined by variance (9) and the matrix of covariance coefficients in formula (7), hence it is expressed by the following formula:

(10)

Cov(X^)=σ02(CX−1+ATPA)−1.

The elements on the diagonal of matrix (10) determine the variances of individual estimated parameters, and their square root is the standard deviation σ(x_i) of these parameters.

In order to determine the significance level of the values of the estimated parameters, it is necessary to estimate the limit value of their standard deviation at the predetermined confidence level (1 − α).

A functional relationship that defines the estimated variance σ² (x_i) of the analysed parameter (x_i) and the tested variance σ2(x↔i) of this parameter, taking into account k = n − u degrees of freedom, is denoted by chi-square (χ²) and takes the following form:

(11)

χ2=k⋅σ2(xi)σ2(x↔i).

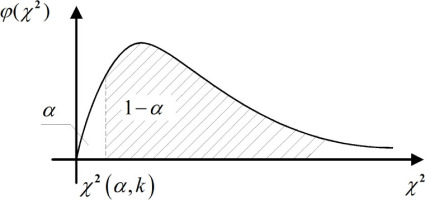
The chi-square distribution can be defined by its quantiles χ²(α; k), determined based on the probability density function and the significance index α. The quantile χ²(α; k) is the length of the abscissa on the axis Oχ², which, from the whole area under the graph of the density function with the area of 1, cuts off the area of α, as illustrated in Figure 1. The surface area of the area marked in Figure 1 satisfies the inequality

χ2>χ2(αi;k),

which expresses probabilities with the value of (1 − α), called the confidence level. This relationship can be written in the following analytical form:

(12)

p[χ2>χ2(αi;k)]=1−α.

Having substituted (11) for χ², the relationship of the estimated variance and the tested variance was obtained, in conjunction with the quantile of the distribution (χ²), that is,

(13)

p[k⋅σ2(x)σ2(x↔)>χ2(αi;k)]=1−α.

The above dependence shall always occur if the expression in square brackets is satisfied, that is,

(14)

k⋅σ2(x)σ2(x↔)>χ2(αi;k).

Transformation of the above inequality leads to the following condition for the tested variance, which is a limit value for the confidence level of (1 − α):

(15)

σ2(x↔)≤k⋅σ2(x)χ2(αi;k).

The interpretation of the above inequality is as follows: at the confidence level of (1 − α), the maximum value of the tested variance will always be less than, or equal to, the estimated variance multiplied by the coefficient k/χ²(α; k). In practical surveys, the standard deviation of the estimated parameters is used, hence formula (15) can be written in the following form:

(16)

σ(x↔)≤kχ2(αi;k)⋅σ(x).

Positive values of the square root of the coefficients k/χ²(α; k), for the selected degrees of freedom from 2 to 10 and the selected confidence levels from 0.99 to 0.60, have been presented in Table 1.

Figure 1

Chi-square distribution quantiles

https://rgg.edu.pl/f/fulltexts/173247/j_rgg-2021-0001_fig_001_min.jpg

Table 1

Coefficients to determine limit standard deviations for the estimated parameters (coordinates of points of the geodetic network

k\(1 − α)	0.99	0.95	0.90	0.80	0.60
k = 2	10.0	4.4	3.1	2.1	1.4
k = 3	5.1	2.9	2.3	1.7	1.3
k = 4	3.7	2.4	1.9	1.6	1.2
k = 5	3.0	2.1	1.8	1.5	1.2
k = 6	2.6	1.9	1.6	1.4	1.2
k = 7	2.3	1.8	1.6	1.4	1.1
k = 8	2.2	1.7	1.5	1.3	1.1
k = 9	2.1	1.6	1.5	1.3	1.1
k = 10	2.0	1.6	1.4	1.3	1.1

From the analysis of formulas (10) and (16), it is evident that selection of the elements of the covariance matrix (C_X) for the estimated parameters of the vector X^ and the weighing matrix (P) for the observation vector (L) has a direct effect on the efficiency of the estimated coordinates of the points of the geodetic control, as well as on their reliability.

3. Gauss-Markov model with random parameters – exemplary uses

The Gauss-Markov model with random parameters can be used in surveying engineering in the following cases:

determining point displacements based on periodic surveys and
establishing geodetic control networks connected to the national spatial reference system.

This research paper presents the principles of using the G-M model with random parameters for adjusting the results of surveys of geodetic control networks connected to the national spatial reference system.

The use of this estimation model leads to the determination of appropriate values of random deviations to the values observed in the geodetic control, taking into account their accuracy weights and, at the same time, it includes appropriate adjustments to the coordinates of the reference points resulting from their covariance matrix. A functional square form, defining the sum of the squares of random deviations to the observed values, also takes into account the sum of the squares of adjustments to the coordinates of the reference points. The specified condition for the minimum of this square form allows determining all parameters of the established geodetic control.

As a result of estimation of the G-M model with random parameters, the most probable random deviations to the observed values are obtained, which form the basis for calculating the adjusted values of the elements observed in a determined control, as well as the adjusted coordinates of the points of this control. Adjustments to the coordinates of the reference points unambiguously fit the national spatial reference system, in which the coordinates of the points of the established geodetic control are determined. The values of these adjustments indicate a degree of mutual inconsistency between the coordinates of the reference points in relation to the observed elements in the geodetic control network.

The accuracy of determining the coordinates of the points of the geodetic control network depends on the sum of squares of random deviations to the observed values and on the values of the coefficients of the covariance matrix obtained during the estimation of the G-M model with random parameters. The limit value of the standard deviation (16) for the determined coordinates of the points of the geodetic control, should be used to determine the accuracy of setting-out an engineering structure, in conjunction with the construction tolerance.

Based on the adjustment of the results of surveys of the national spatial reference system, the vector of the coordinates of all the points is obtained, and the covariance matrix for this vector takes the following form in the symbolic matrix record:

(17)

X^N=[x1y1z1…]⇔Cov[X^N]=[V(x1)cov(x1,y1)cov(x1,z1)…cov(x1,y1)V(y1)cov(y1,z1)⋮cov(x1,z1)cov(y1,z1)V(z1)⋮…………]

If, for example, two reference points of the national spatial reference system are used to adjust the horizontal geodetic control network then, from the entire covariance matrix (17), it is necessary to select four blocks of the sub-matrices (of the size 2×2), which correspond to the reference points. If the reference points are denoted, for example, by numbers 2 and 4, then the corresponding covariance matrix will take the following form:

(18)

X^NT=[x2y2x4y4]⇔Cov[X^NT]=[V(x2)cov(x2,y2)cov(x2,x4)cov(x2,y4)cov(y2,x2)V(y2)cov(y2,x4)cov(y2,y4)cov(x4,x2)cov(x4,y2)V(x4)cov(x4,y4)cov(y4,x2)cov(y4,y2)cov(y4,x4)V(y4)]

The system of observation equations for the elements of the geodetic control network should take into account all the points of the established control and the reference points. The form of this system of equations, in a symbolic matrix record, is as follows:

(19)

δ=AX=L.

According to the denotations for formula (19):

δ – represents the vector of random deviations to the observed elements of the geodetic control network,
A – is the matrix of coefficients at estimated unknowns,
X – represents the vector of unknowns, containing adjustments to the coordinates of the points of the geodetic control network and the reference points and
L – denotes the vector of absolute terms, that is, differences between the values of the observed elements and their approximate values.

To create the observation equations (19), a diagonal weighting matrix P should be defined, whose values of the elements result from the accuracy of surveys of the geometric elements in the geodetic control. Based on this system of equations, a system of normal equations can be developed, the form of which is as follows:

(20)

(ATPA)⋅X=ATP⋅L.

The above system of equations will always have a defect because the determinant from the matrix (A^T PA) will be equal to zero. The inverse of the covariance matrix [Cov(X^NT)]−1 for the coordinates of the reference points will be used to eliminate this defect.

The matrix [Cov(X^NT)]−1 , supplemented by zeros to the size of the matrix (A^T PA), leads to the matrix CX−1 . If we add the matrix CX−1 to the matrix (A^T PA), then we get a system of equations in the form (6), which implements estimation of the G-M model with random parameters, that is,

(21)

[CX−1+ATPA]⋅X^=ATP⋅L.

The dependence (21) forms the basis for deriving the final formula for calculating the estimator of the vector X^ in the following form:

(22)

X^=[CX−1+ATPA]−1⋅ATP⋅L.

The covariance matrix for such a vector of unknowns, or the estimated coordinates of the points of the geodetic control network and the reference points, is expressed by the formula

(23)

Cov(X^)=σ02[CX−1+ATPA]−1.

The parameter σ02 represents the variance determined based on the obtained random deviations to the observed values, that is,

(24)

σ02=δTpδn−u,δ=L−AX^.

Based on the coefficients presented in Table 1, the limit values of the standard deviation for the determined coordinates of the points can be specified.

4. Numerical example of using Gauss-Markov model with random parameters

In order to verify the principles of estimation of the G-M model with random parameters, the simplest structure of the geodetic network of points was selected, in which all the observations regard differences in elevations only. The analysed fragment of the levelling network of points consists of three points making up the geodetic control network and two reference points representing the national spatial reference system, as illustrated in Figure 2.

Figure 2

A fragment of levelling network of points

https://rgg.edu.pl/f/fulltexts/173247/j_rgg-2021-0001_fig_002_min.jpg

In the analysed network of points, five elevation differences h_i were measured using the appropriate number of the level n_i stands. The reference points A and B, with given elevations, have the following covariance matrix and its inverse:

(25)

Cov[zA,zB]=[0.810.200.200.64][mm2]⇔(Cov[zA,zB])−1=[1.34−0.42−0.421.69][1mm2].

To adjust the survey results, it was predetermined that for the elevation difference observed from one-level stand, the standard deviation is equal to 0.2 mm. Using the principle of adding the variances, the variance σi2 and weight p_i were calculated for each observed elevation difference:

σ12=0.16 mm2p1=6.25,σ22=0.20 mm2p2=5.00,σ32=0.32 mm2p3=3.12,σ42=0.08 mm2p4=12.5,σ52=0.16 mm2p5=6.25.

The observation equations for measured elevation differences h_i always have a linear form, and therefore their differential form is as follows:

(26)

δi+dziK−dzip=hi−(z˜iK−z˜ip).

The right side of Equation (26), containing the observed elevation differences and approximate elevations of the points of the geodetic control, as well as the exact elevations of the reference points, is an absolute term. The elevations of the reference points and the approximate elevations of the points of the geodetic control are as follows:

zA=1.108 m;z˜1=1.200 m,zB=1.406 m;z˜2=1.280 m,z˜3=1.250 m,

Based on the results of the levelling surveys demonstrated in Figure 2, five observation equations can be developed, which will contain five unknowns representing adjustments dz_i to two reference points and three points of the geodetic control network.

(27)

δ1+dz1−dzA=h1−(z˜1−z˜A),δ2+dz2−dz1=h2−(z˜2−z˜1),δ3+dzB−dz2=h3−(z˜B−z˜2),δ4+dz3−dzB=h4−(z˜3−z˜B),δ5+dz1−dz3=h5−(z˜1−z˜3),

Having taken into account the system of equations (27) and the schedule of observations, the matrix A of coefficients with the unknowns, the matrix L of absolute terms, and the weighing matrix P take the following form:

A=[−1010000−110010−10000−110010−1], L=[8.03.2−7.6−0.8−1.5] [mm],p=[6.25000005000003.120000012.5000006.25].

The values of the elements of the above-mentioned matrices were used to implement formulas (18)–(21), which led to the following calculation results:

CX−1=[1.34−0.42000−0.421.69000000000000000000],ATPA=[6.250−6.250003.120−3.120−6.25017.5−5−6.250−3.12−520.62−12.500−6.25−12.518.75],CX−1+ATPA=[7.59−0.42−6.2500−0.424.810−3.120−6.25017.5−5−6.250−3.12−520.62−12.500−6.25−12.518.75],[CX−1+ATPA]−1⋅ATP=[−0.0594−0.0405−0.11900.01350.02700.04300.02930.0862−0.0098−0.01960.0850−0.0511−0.15030.01700.03410.07430.0507−01716−0.0169−0.03380.07790.0167−0.16450.0478−0.0645],X^=[CX−1+ATPA]−1ATP⋅L=[−1,180,866,509,088,19].

The calculated values of the vector X^ form the basis for determining the most probable elevations of the points of the geodetic control network, that is,

z^1=1.200+0.0065=1.2065 m,z^2=1.280+0.0091=1.2891 m,z^3=1.250+0.0082=1.2582 m.

Adjustments to the elevations of the reference points with the values of −1.18 mm and 0.86 mm prove that, with reference to the performed and adjusted observations in the geodetic control network, the elevations of these points are inconsistent with each other at the level of their difference, that is, 2.04 mm. The most probable random deviations δ to the observed point elevation differences take the following values:

δ=L−AX^=[0.30.60.60.10.2] [mm],σ02=4.0785−3=2.04 mm2.

The adjusted elevation differences, which make up the geodetic control observation programme, are the differences between their observed values and random deviations, that is,

h^1=100.0−0.3=99.7,h^2=83.2−0.6=82.6,h^3=118.4−0.6=117.8,h^4=−30.8−0.1=−30.9,h^5=−51.5−0.2=51.7.

The covariance matrix for the estimated parameters X^ takes the values

CovX^=2.04⋅[0.580.360.520.480.500.360.520.410.440.430.520.410.610.560.580.480.440.560.610.590.500.430.250.590.64] [mm2].

The elements on the diagonal of the above matrix are the squares of standard deviations for the elevations of the reference points and points of the geodetic control network, therefore

[σ(z^1)σ(z^2)σ(z^3)]=[1.111.111.14][mm].

Based on the values presented in Table 1, for k = 5 − 3 = 2 and (1 − α) = 0.90, the coefficient k/χ2(α;k)=3.1 was determined, which defines the limit value of the standard deviation for the estimated parameters. Thus, the limit values of the standard deviation for the determined elevations of the points of the geodetic control network are at the level of

[σ(z↔1)σ(z↔2)σ(z↔3)]=3.1⋅[1.111.111.14][mm]

The above relationship proves that point number 3 gets the largest limit value of the standard deviation, which is at the level of 3.5 mm. Therefore, the determined geodetic control network can be used to set out elevations of points defining structural elements of the building's design, for which the limit construction tolerance is greater than 3.5 mm.

5. Final remarks

The proposed algorithm for the estimation of the G-M model with random parameters for adjusting results of surveys of geodetic control networks connected to the national spatial reference system allows determining the most probable random deviations to the observed values, which constitute the basis for calculating adjusted values of the elements observed in the determined control network, as well as adjusted coordinates of the points of this control. Adjustments to the coordinates of the reference points unambiguously define the national spatial reference system in which the coordinates of the points of the established geodetic control network are determined. The values of these adjustments define a degree of mutual inconsistency of the coordinates of the reference points in relation to the observed elements in the geodetic control network. The accuracy of determining the coordinates of the points of the geodetic control network depends on the sum of squares of random deviations to the observed values, and on the values of the covariance matrix coefficients obtained during the estimation of the G-M model with random parameters. The limit value of the standard deviation, for the determined coordinates of the points of the geodetic control network should be used to determine the accuracy of setting out an engineering structure, in conjunction with the construction tolerance.

eISSN:	2391-8152
ISSN:	2391-8365