. Introduction

In the research of Lityns’kyy et al. (2014), the theoretical solution to the direct problem was found – calculation of optimal values of the measured distances for the accurate determination of the small segments’ lengths. In the research of Lityns’kyy et al. (2015), the methodology was practically tested, with the electronic tacheometers (with characteristics mS = 2 mm, mβ = 500), determined the length of one-meter and ten-meter dimensional segments with an accuracy of 0.2–0.8 mm. In this proposed research, the inverse problem is solved: ‘Optimization of determining the coordinates of an unknown point for a fixed basis in order to provide a high-precision geodetic binding’. This allows us to design a network of reference points to obtain the highest accuracy of the position of the desired point. Depending on the distance selected between the reference points, the accuracy of determining of the position of the desired point can vary considerably for the basic indicators of accuracy of measuring lines and angles. Classically in geodesy, the method of determining the coordinates of an unknown point at measured angles and distances to known points is called reverse linear angular intersection. When measuring angles, distances and their combinations, the reverse intersections are divided into: angular, linear and angular-linear. Mathematically, the problem is unambiguously solved if two angles are measured for angular intersection, one angle and one distance for linear-angular intersection and two distances for linear intersection. Geodesically, additional (redundant) measurements are performed to assess accuracy. The form of a triangle formed during the measurement of angles, lines, angles and lines affects the accuracy of the determination of the desired point. Of particular interest is the linear-angular intersection,

since it can use combinations of measurements.

The research of Gargula (2009) presents the theoretical and empirical studies of the accuracy of the angle determination in a triangle using the law of sines, if the angle is close to the direct one. The research is done for use in geodesy (for example, to determine the coordinates), which requires a certain level of accuracy. Several models have been researched for various triangular variants, on the basis of which a ‘safe’ angle was determined.

Nowadays, there are several methods for evaluating the accuracy of the inverse linear-angular intersection. We have proposed a method for determining the position of an unknown point P, which provides an opportunity to predict the accuracy of determining its coordinates, depending on the distance between the reference points, the distance to the desired point and the accuracy of the device used.

Such studies are of interest to high-precision engineering and geodetic works, where apriori it is necessary to know the possible accuracy of the instrument’s coordinates (Vivat et al., 2018) for planning the locations of the installation of an electronic tacheometer or a laser scanner.

. Mathematical research

The coordinates of an unknown point P are calculated as:

(1)
xp=x0+Δxyp=y0+Δy

where:

xP, yP – coordinates of an unknown point,

x0, y0 – coordinates of a known point,

Δx,Δy – increase of coordinates.

Let‘s find out the values of the measured parameters S1, S2 and β when the error of the calculation of coordinates will be minimal. In this case, one side of the formed triangle S is fixed (Fig. 1).

Figure 1

Regarding the theory of coordinate determination using the planar linear-angular intersection method

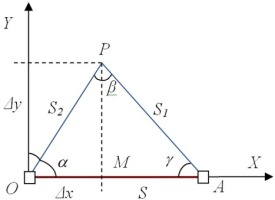
https://rgg.edu.pl/f/fulltexts/173264/j_rgg-2019-0003_fig_001_min.jpg

For the measured two sides of the triangle and the angle between them, the increase of coordinates Δx and Δy can be calculated by various methods, for example, by the law of sines and cosines, and also the Pythagorean theorem (Shkil, 2005). Let’s write down these formulas in a sequential manner.

Law of sines:

(2)
α=arcsin(s1ssinβ),
(3)
γ=arcsin(s2ssinβ).

Let‘s determine the increase of the coordinates Δx by using the value of the angles from the formulas (2) and (3):

(4)
Δx=s2cos⁡α=s21−s12sin2βs2=s2ss2−s12sin2β,
(5)
Δx=s−s1cos⁡γ=s−s1ss2−s22sin2β.

By the Pythagorean theorem, we define the increase Δx for the acute and obtuse angle:

(6)
Δx=−S12+S22+S22S.

The increase in Δy for all cases can be determined by one formula:

(7)
Δy=S2sinα=S1S2sin βS,

With corresponding mean square error of:

(8)
my2=1S2S22sin2β⋅mS12+S12sin2β⋅mS22+S12S22cos2β⋅mβ2.

Additionally, from the triangle OPM we also calculate:

(9)
Δy=S22−(Δx)2.

Therefore, it is important to choose such formulas for which there are no peculiarities and which have the slightest error in finding the coordinates of point P. For this, we will write down formulas of mean square errors for different cases.

Using formulas (4)–(6) gives three cases of calculation of the value mx2:

(10)
mx2=1s2S2−S12sin2βmS22+S22S12sin4β⋅mS12+S14sin2βcos2β⋅mβ2S2−S12sin2⁡β,mx2=1S2S2−S22sin2βmS12
(11)
+S12S22sin4 β⋅mS22+S24sin2 β cos2 β ⋅ mβ2S2−S22sin2 β), 
(12)
mx2=S12mS12+S22mS22S2.

Mathematically, the problem is to find the minimum error of:

(13)
mp2=mx2+my2

providing

(14)
S2=S12+S22−2S1S2cos β,

is formulated as finding the minimum of the Lagrange function:

(15)
F(S1,S2,β)=mx2+my2+λ(S12+S22−2S1S2cos β−S2).

Analysis of the two formulas for the calculation of errors (10), (11) reveals a feature (Fig. 2), namely:

Figure 2

Peculiarity of determination of coordinates by law of sines

https://rgg.edu.pl/f/fulltexts/173264/j_rgg-2019-0003_fig_002_min.jpg
limmx2→∞,

for

sin⁡β→SS1S1≥S,sin⁡α→1,α→π2,Δx→0,S1→S,mx→∞

in formula (10), and

sin⁡β→SS2S2≥S,sin⁡γ→1,γ→π2,Δx→0,S2→S,mx→∞

in formula (11).

Also, by tabulating functions (10) and (11) it is established that for the given S1, S2, fixed basis S and a definite angle β, there is no extremum by the law of cosines.

We perform the analysis of formulas (8, 12, 13). For the graphical and tabular representation of the values of formula (13), we use the software (Wolfram Mathematics). Figures 3– 5 presents the accuracy of determining the position of the point P, depending on the length of the base segment and the accuracy of the measurement of angles and lines. The values of the accuracy of the determination of coordinates in the characteristic points of Pi are also given in Tables 1–3.

Figure 3

The accuracy of determining the point P for S = 100 m, mS = 1 mm, mβ = 1"

https://rgg.edu.pl/f/fulltexts/173264/j_rgg-2019-0003_fig_003_min.jpg
Figure 4

The accuracy of determining the point P for S = 3000 m, mS = 1 mm, mβ = 1"

https://rgg.edu.pl/f/fulltexts/173264/j_rgg-2019-0003_fig_004_min.jpg
Figure 5

Accuracy of determining the point P for S = 300 m, mS = 0.1 mm, mβ = 1"

https://rgg.edu.pl/f/fulltexts/173264/j_rgg-2019-0003_fig_005_min.jpg
Table 1

The value of mP of nine characteristic points for Fig. 3

Pointx [m]y [m]S1 [m]S2 [m]mP [mm]
b10.00.0S =100 m
b20.0100.0mS = 1 mm , mβ = 1n
p10.050.050.050.01.0
p250.050.070.770.71.5
p3100.050.0111.8111.82.2
p4100.00.0141.4100.02.3
p50.0-50.0150.050.01.5
p60.0-100.0200.0100.02.5
p7-100.00.0141.4100.02.2
p8-100.050.0111.8111.82.0
p9-50.050.070.770.71.5
Table 2

The value of mP of nine characteristic points for Fig. 4

Pointx [m]y [m]S1 [m]S2 [m]mP [mm]
b10.00.0S = 3000 m
b20.03000.0mS = 1 mm, mβ = 1}
p10.01500.01500.01500.03.4
p21500.01500.02120.02120.02.0
p33000.01500.03354.03354.013.0
p43000.00.04242.03000.014.0
p50.0-1500.04500.01500.011.0
p60.0-3000.06000.03000.025.0
p7-3000.00.04242.03000.014.0
p8-3000.01500.03354.03354.012.0
p9-1500.01500.02120.02120.02.0
Table 3

The value of mP of nine characteristic points for Fig. 5

Pointx [m]y [m]S1 [m]S2 [m] mP [mm]
b10.00.0S = 300 m
b20.0300.0mS = 0.1 mm, mβ = 1n
p10.0150.0150.0150.00.4
p2150.0150.0212.0212.00.2
p3300.0150.0354.0354.02.2
p4300.00.0424.0300.01.3
p50.0-150.0450.0150.01.1
p60.0-300.0600.0300.02.1
p7-300.00.0424.0300.01.4
p8-300.0150.0353.0353.01.1
p9-150.0150.0212.0212.00.2

Table 1 gives the accuracy of determining the coordinates of the point P for the characteristic discretely selected nine points for S = 100 m, mS = 1 mm, mβ = 1} from Fig. 3a. Columns 4 and 5 also show the values of the formed sides S1 and S2.

Table2 gives the accuracy of determining the coordinates of the point P for the characteristic discretely selected nine points for S = 3000 m, mS = 1 mm, mβ = 1} from Fig. 4a.

Table 3 gives the accuracy of determining the coordinates of the point P for the characteristic discretely selected nine points for S = 300 m, mS = 0.1 mm, mβ = 1} from Fig. 5a.

For Figs 4 and 5, an interesting dependence of the accuracy of the determination of the coordinates of a point P is observed. If the point P is placed on a circle with a diameter equal to the base S, then the accuracy of the mP is the same for all the points that are on the diameter.

. The formula derive for determining the optimal position

Let’s try to analytically derive the formula for determining the optimal position of point P. We will write a function for which it is necessary to determine the minimum:

(16)
F(S1,S2, β)=1S2((S12+S22sin2 β)mS12)+(S22+S12sin2  β)mS22                 +(S12S22cos2 β)mβ2) +λ(S12+S22−2S1S2cos β−S2). 

Assume that mS12=mS22.Accordingly, the function:

(17)
FS1,S2,β=1S2S12+S221+sin2βmS12+S12S22cos2βmβ2+λS12+S22−2S1S2cos⁡β−S2.

Let’s write the conditions for the existence of an extremum:

(18)
{∂F∂S1=2S1S21+sin2βmS12+S22cos2βmβ2+2λS1−S2cosβ=0∂F∂S2=2S2S21+sin2βmS12+S12cos2βmβ2+2λS2−S1cosβ=0.∂F∂β=sin⁡2βS2S12+S22mS12−S12S22mβ2+2λS1S2sin⁡β=0S2=S12+S22−2S1S2cosβ

Let’s note k=mS12mβ2.Accordingly, the system of equation (18) could be rewritten as:

(19)
{S1mβ2S21+sin2βk+S22cos2β+λS1−S2cosβ=0mβ2S21+sin2βkS1−S2−S1S2cos2βS1−S2+λS1−S21+cos⁡ β =0sin⁡ β cos⁡ β m β 2S2S12+S22k−S12S22+λS1S2=0S2=S12+S22−2S1S2cos⁡ β 

or

(20)
{S1m β 2S21+sin2 β k+S22cos2 β + λ S1−S2cos⁡ β =0S1−S2m β 21+sin2 β k−S1S2cos2 β S2+ λ 1+cos⁡ β =0Sin⁡ β cos⁡ β m β 2S2S12+S22k−S12S22+ λ S1S2=0S2=S12+S22−2S1S2cos⁡ β 

The second equation of the system (20) splits into two. For

S1 = S2 we have:

(21a) (21b) (21c)
{S1(mβ2S2((1+sin2β)k+S12cos2β))=−λS1(1−cosβ)sinβ(cosβmβ2S2((2S12k)−S14))=−λS12sinβS2=2S12−2S12cosβ=0

Assuming that sin β ≠ 0 (not a degenerative case), we obtain from the first two equations of the system (21a):

(22)
(1+sin2β)k+S12cos2βcosβ(2k−S12)=1−cosβ

Therefore, taking into account (21c), equation (22) will have the following form:

(23)
2(1−cosβ)(1+sin2β)k+S2cos2βcosβ(2k−S22(1−cosβ))=2(1−cosβ)2

The solution (23) is determined by one of the approximate methods, for example, by the bisection method. The results of calculations show the existence of a minimum error value only for certain bases shown in Figures 3– 5.

. Closing remarks

The determination of the point coordinates for a fixed basis is possible with different formulas.

The measurement error of the calculations for some methods does not accept optimal values, but varies in the range from infinity to a fixed value.

Only the combined method of determining the coordinates can optimize the measurement error of the calculations.

It is established that the constant error of calculations is achieved when placing a device in a circle whose diameter is equal to the basis S.

The value of this error is determined by the formula:

m2(π2)=2ms2.

There is a dependence between the basis and the accuracy of measurements, which is established on the basis of an approximate solution of the equation.