1. Introduction

Land and urban management require detecting changes in topography and urban areas. Topography changes in rural areas are generally the results of natural processes such as landslides, earthquakes, coastal erosion de- or afforestation. Urban changes consist of new constructions, extensions, destructions, excavation work and earth fill formed by natural or human effects. Change detection in urban areas is essential for planning, management, building and discovering unauthorized construction activities. In addition, the results of earthquakes can be detected very quickly, and first aid can reach vital regions. Changes in topography of urban areas refer to changes in their digital elevation model (DEM), which can be detected by comparing the time period DEMs. A significant amount of information, such as the area, volume, cross section and slope of the earth’s surface, can also be extracted from DEMs.

The key issue in the creation of a three-dimensional (3D) model and DEM is acquiring high-density 3D spatial data that represent the object’s shape. High-density spatial data with short-space 3D points from land or object surfaces are called point clouds. Point clouds of land surfaces can be obtained from LiDAR (light detection and ranging), SAR (synthetic aperture radar) or photogrammetry from stereo or multiview images. The point space of aerial and terrestrial LiDAR depends on the technical specification of the instrument (Ghuffar et al., 2013). LiDAR has a sufficient level of measurement accuracy but requires expensive procedures. Thus, LiDAR cannot be applied to every measurement task. SAR is applied by satellite and measures the earth’s surface at particular (1–3 m) grid intervals (Bildirici et al., 2009). The accuracy of a DEM model created by SAR is lower than that created by LiDAR and is approximately 40 cm. However, image based dense point cloud by using structure-from-motion (SfM) algorithm enables highly accurate point cloud acquisition from stereoscopic images. The stereoscopic images are recorded by aerial camera from aerial platforms such as airplane, helicopter, or unmanned aerial vehicle (UAV) or by terrestrial cameras. The automatic methods are applied to SfM algorithm, and an image-based point cloud is generated with short-time processes in a cost-effective manner. Image-based point clouds have been created for many high-accuracy 3D measurement tasks (Ros-nell and Honkavaara, 2012; Haala, 2011). The overall performance of point cloud generation from stereoscopic images is high. Typically, point clouds can be derived even from a single stereo model with the point density corresponding to the ground sampled distance (GSD). The height accuracy is dependent on the object properties and the intersection geometry, and it is 0.5–2 times GSD for well-defined objects. The development of interpretation methods that are insensitive to shadows is important to enable optimal use of photogrammetric technology (Honkavaara et al., 2012). Photogrammetry shares the advantages of LiDAR with respect to point density, accuracy and cost (Leberl et al., 2010). However, excessive images increase the processing time when creating point clouds. This problem could be solved by optimization (Ahmadabadian et al., 2014; Alsadik et al., 2013).

Dense point clouds have been created from multiview stereoscopic images in many applications such as mapping, visualization, 3D modelling, DEM creation, and natural hazard detection. Yang et al. (2013) exploited dense image matching for 3D modelling of indoor and outdoor objects. Tree heights were also estimated by DEM created from dense point clouds of UAV images (Jensen and Mathews, 2016). The same task was performed with LiDAR point clouds, and a comparison of their point-cloud-based DEMs showed 19 cm variances. In addition, point clouds have been created from aerial and UAV images for detecting the effects of natural disasters in agricultural areas (Cusicanqui, 2016). New buildings in urban areas have also been detected using image-based and LiDAR point clouds (Nebiker et al., 2014; Hebel et al., 2013). A similar study was carried out to compare the point clouds of historical aerial images and new LiDAR data (Du et al., 2016). A comparison of point clouds based on satellite imagery and LiDAR highlighted changes including small-scale (<50 cm), sensor-dependent, large-scale, and new home construction (Basgall et al., 2014).

In this study, urban changes in the city centre of the Konya metropolitan area, Turkey, were visualized by comparing the point clouds of multiperiod historical aerial images. Historical images from 1951, 1975, 1998 and 2010 were procured from the archive of General Command of Mapping (HGK) in Turkey. In addition, urban changes in density and degrees over the investigated historical periods were analysed. The rest of the paper consists of five sections. The related historical studies are described in section 2, and the study area is described in section 3. Section 4 introduces image-based point cloud creation and change detection procedures. The results related to point cloud creation, geo-registration, change detection and their analysis are given in section 5. A discussion and conclusion are provided in section 6 and section 7, respectively.

2. Related work

Photogrammetry has been put into practice in many types of studies such as object modelling (Lingua et al., 2003), accident recovery (Fraser et al., 2005), natural hazard assessment (Al-tan et al., 2001), deformation measurement (Jiang et al., 2008), industrial imaging (Cooper and Robson, 1990), and space research (Di et al., 2008). The photogrammetric processes have been changed together with the scientific progress. In particular, developments in computer vision techniques and the introduction of new keypoint detection operators such as scale-invariant feature transform (SIFT), speeded-up robust features (SURF), binary robust independent elementary features (BRIEF) and Affine-SIFT (ASIFT) have contributed to the automatization of photogrammetric processes. These new generation key-point detectors automate image matching despite scale, orientation and lighting differences between stereoscopic images. The SIFT keypoint detector was first introduced in early 2000 (Lowe, 2004). Other keypoint operators have been introduced to improve the weak ability of SIFT and its application to different tasks. The first variety of SIFT is the SURF algorithm, which defines keypoints with lower-dimensional feature vectors for fast evaluation (Bay et al., 2006). Although SURF has a lower-dimensional feature vector, images can be matched by SURF with an accuracy similar to that of images matched by SIFT (Altuntas, 2013). In addition, BRIEF reduced the memory requirement with respect to SIFT (Calonder et al., 2010). SIFT does not consider Affine deformation between images when detecting keypoints. ASIFT is obtained by varying the two camera axis orientation parameters – namely, the latitude and the longitude angles – which are not treated by the SIFT method. Thus, ASIFT was introduced for effectively covering all six parameters of the Affine transform (Yu and Morel, 2011).

Keypoint detection operators associate a descriptor with each extracted image feature. A descriptor is a vector with a variable number of elements that describes the keypoint. Homologous points can be found by simply comparing the descriptors, without any preliminary information about the image network or epipolar geometry (Barazzetti et al., 2010). The automatically extracted image coordinates of conjugate keypoints can be imported and used for image orientation and sparse geometry reconstruction. The matching results are generally sparse point clouds, which are then used to grow additional matches. These procedures, which include camera calibration, image ordering and orientation, are called SfM or multi-view photogrammetry in the computer vision community. Dense point cloud is generated from the image block that was oriented and motion estimated by SfM algorithm. The dense 3D surface reconstruction is increasingly available to both professional and amateur users whose requirements span a wide variety of applications (Ahmadabadian et al., 2013).

Dense point clouds can represent small object details owing to high-density 3D spatial data. The colour recorded for the measured points and the texture mapping of mesh surfaces distinguishes dense image-based measurements. Thus, dense image-based point clouds are especially useful for documenting cultural structures (Barazzetti et al., 2010). Object modelling and topography measurement are also performed with dense point clouds created from aerial or ground-based images (Aicardi et al., 2018; Rossi et al., 2017). The unmanned aerial vehicle based image acquisition has increased the popularity of dense image-based modelling (Haala and Rothermel, 2012).

The accuracy of image-based dense point cloud depends on the imaging geometry. The appropriate image geometry has about 1 base/height ratio, which enables high-accuracy measurements (Haala, 2011; Remondino et al., 2013). Its comparison with terrestrial LiDAR has shown a 5 mm standard deviation (Barazzetti et al., 2010). The accuracy related to different types of land cover was compared to LiDAR measurement, and a similar degree of accuracy was obtained (Zhang et al., 2018). Furthermore, UAV photogrammetric data were found to capture elevation with accuracies, by root mean square error, ranging from 14 to 42 cm, depending on the surface complexity (Lovitt et al., 2017).

The number and distribution of ground control points (GCPs) affect both the scale and geo-referencing accuracy of adense point cloud model. Geo-referencing with GCPs that were signalized before the imaging area was performed with accuracy of a few centimetres, and more GCPs did not improve the geo-referencing accuracy (Zhang et al., 2018). If the GCPs had not been signalized on the imaging area, the registration would have been performed by the detail-based GCPs selected and measured after capturing the images. UAV image data were registered to the geo-reference system by using the detail-based GCPs with decimetre-level root mean square error (RMSE) of coordinate residuals on GCPs. Similarly, historical aerial images were geo-referenced by detail-based GCPs with approximately 4 m RMSE on residuals of GCPs (Nebiker et al., 2014; Hughes et al., 2006). At least six object-based GCPs assured a sufficiently high accuracy for the geo-referencing of historical aerial images (Hughes et al., 2006). Generally, height residuals that correspond to Z coordinates are three times larger than the horizontal level of the XY plane.

The changes of land topography, forests and urban areas can be detected with the analyses of point cloud data from LiDAR or SfM photogrammetry. Significant forest canopy changes were detected from the image-based point clouds. Image based dense point cloud is preferable with respect to the other measurement techniques for change detection in forest areas (Ali-Sisto and Packalen, 2017). In another study, a methodology for automatically deriving change displacement rates in a horizontal direction based on comparisons between the extracted landslide scarps from multiple time periods was developed. Horizontal and non-horizontal changes were detected by the proposed method with a RMSE of approximately 12 cm (Al-Rawabdeh et al., 2017). In addition, landslide changes were detected from LiDAR point clouds with 50 cm point spaces using a support vector machine through three axis directions at 70% accuracy (Mora et al., 2018). Furthermore, a terrestrial photogrammetric point cloud for landslide change detection was tested, and the accuracy of the resulting models was assessed against the terrestrial and airborne LiDAR point clouds. It could be demonstrated that terrestrial multi-view photogrammetry is sufficiently accurate to detect surface changes in the range of decimetres. Thus, the technique currently remains less precise than TLS or GPS but provides spatially distributed information at significantly lower costs and is, therefore, valuable for many practical landslide investigations (Stumpf et al., 2015; James et al., 2017).

Urbanisation creates many changes such new constructions or demolitions of buildings, land use and land cover changes. These changes can be detected by comparing two point clouds, which should be processed for further information to define the changes. Awrangjeb et al. (2015) offered a new or demolished building change detection technique from LiDAR point cloud data. The proposed technique examines the gap between neighbouring buildings to avoid under-segmentation errors. In another study, the acquisition of changed objects above ground was converted into a binary classification, in which the changed area was regarded as the foreground and the other area as the background. After the image-based point clouds of each period were gridded, the graph cut algorithm was adopted to classify the points into foreground and background. The changed building objects were then further classified as newly built, taller, demolished and lower by combining the classification and the digital surface models of the two periods (Pang et al., 2018). Barnhart and Crosby (2013) used clouds to mesh comparisons and a multiscale model to the cloud comparison in terrestrial laser scanning data of topographic change detection. Xiao et al. (2015) proposed point-to-triangle distance from combined occupancy grids and a distance-based method for change detection from mobile LiDAR system point clouds. The combined method tackles irregular point density and occlusion problems and eliminates false detections on penetrable objects. Tran et al. (2018) suggested a machine learning approach for change detection in 3D point clouds. They combined classification and change detection into one step, and eight different objects were classified as changed and unchanged with overall accuracy over 90%. Vu et al. (2004) offered regular grid data for an automatic change detection method to detect damaged buildings after an earthquake in Japan. Scaioni et al. (2013) also used regular grid point cloud data for detecting changes by comparing grid patches. The iterative closest point (ICP) algorithm and its variants were also employed to detect the changes between the two point clouds. The change detection method was proposed by Zhang et al. (2015) as a weighted anisotropic ICP algorithm, which determined the 3D displacements between the two point clouds by iteratively minimizing the sum of squares of the distances. They estimated earthquake changes by evaluating pre- and post-LiDAR data.

The contribution of this study is the visualization of urban changes by comparing image-based point clouds of the two periods using the ICP algorithm and analysing the changes of ordinary time periods.

3. Study Area

Konya city, which was the capital of Seljuk Empire, is located at the centre of Anatolia. The city has many historical structures such as caravansary, mosque, fountain, madrasah and mausoleum. Moreover, it has Mevlana Museum and Rumi mausoleum, which are attractive destinations for tourists from all over the world. On the other hand, Konya city has many industrial plants that have grown over the years. Therefore, the population in Konya metropolitan area has recently increased very fast.

The study area was defined by a rectangle with cross-corner of geographical coordinates of 37°53’26.67"N latitude, 32°28’37.38"E longitude and 37°52’38.30"N latitude, 32°29’39.11"E longitude. Its dimensions are 1.5 km × 1.5 km, or 2.25 km². It largely includes houses and trade buildings, but it also includes tramway and railway networks, asphalt pavement, green fields and cemetery areas of Musalla (Figure 1).

Figure 1

Visualization of the study area

4. Material and Methods

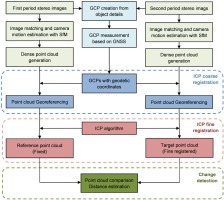
Urban changes can be visualized by comparing the DEMs created with image-based point clouds of time series images. Here, the point clouds were registered to a geo-reference system using GCPs, and they were compared after fine-registering with the ICP algorithm. Actually, geo-referencing procedure registers all the point cloud data in the same coordinate system for change detection. However, their registrations still include a small error due to object based GCPs in geo-referencing. Thus, relative fine registration was performed by ICP for eliminating registration errors and accurate pairwise comparison. The differences between each two point clouds represent the changes from the beginning to the end of the interest period. The main progressive steps of this study are shown in Figure 2.

Figure 2

Workflow of the applied change detection method

Ground control points

The GCPs were used for the geo-referencing of dense point clouds created from historical aerial images. The images do not include GCPs signalized in the imaging area before taking the images. Thus, the GCPs were produced from significant object details for geo-referencing. The object-based GCPs should be selected from the images and should be existing in situ. Building corners, fences, crossroads, and so on, with these properties were used to create the object-based GCP (Figure 3). Therefore, every GCP could not be seen in the stereoscopic images of every period, so different GCPs were used for the geo-referencing of time series image-based point clouds. Object-based GCP creation is usually very hard in non-building areas, such as visible in the case of the oldest images from 1951 in this study. Nevertheless, because Konya has many historical structures that are suitably positioned for creating GCPs, enough GCPs can be created. A total of twenty-two GCPs were established, and their geodetic coordinates were measured based on the global navigation satellite system (GNSS). Absolute positional accuracy of GCPs is about 10 centimetres. Geo-referencing with GCPs ensures both integration with the geodetic coordinate system and scaling for the 3D point cloud

Figure 3

The examples from object-based GCPs

model. The scale can also be established by the ratio of distances among the same points in the object and model spaces (Barazzetti et al., 2010; Hartley and Zisserman, 2003). Ahmadabadian et al. (2013) benefited from base distance to solve the scale problem in automatic image matching and dense point cloud creation. In addition, direct geo-referencing is performed with imaging positions recorded on the fiy, but its accuracy is lower than geo-referencing with GCPs (Pfeifer et al., 2012; Gabrlik, 2015).

Fine registration with ICP algorithm

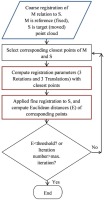
The geo-referencing of the point clouds enables us in detecting the change between them. However, relative fine registration of two point clouds enhances change detection accuracy by removing the small geo-referencing errors that occurs due to the object based control points. The fine registration is implemented by ICP algorithm. One of the overlapping point clouds is selected as a reference, and the other (target point cloud) is oriented and translated in relation to the reference. After the closest conjugate points between the reference and target point cloud are selected by the Euclidean distances, the registration parameters are estimated with these conjugate points. The estimated registration parameters are applied to the target point cloud. These steps are applied iteratively until the RMSE of the Euclidean distances between the corresponding points are smaller than a threshold value or the iteration reaches a certain number (Figure 4). At first, the initial coarse registration must be implemented by interactive or computational approaches. In this study, geo-referencing results were accepted as coarse registration of the point clouds. Depending on the coarse registration, the fine registration is performed after 15 or 20 iterations (Besl and McKay, 1992). ICP provides high-accuracy in registration, and varying the density of reference and target point clouds does not affect the registration accuracy (Altuntas, 2014).

Figure 4

Flowchart of the point cloud registration by the ICP algorithm

5. Results

Geo-referencing

All point cloud data was registered to the geo-reference system using at least six GCPs. After these, the GCP coordinates were recomputed by applying the estimated registration parameters. The residuals between the measured and estimated coordinates of the GCPs were exploited to evaluate the registration accuracy. The residuals (Figure 5) and their RMSEs (Table 3) indicated high accuracy for the geo-referencing. The accuracy was better than the object-based geo-referencing presented in the literature (Nebiker et al., 2014; Hughes et al., 2006). Moreover, the max-reprojection errors were at the one-pixel level.

Figure 5

The GCP locations and error estimates on point clouds of a) 1951, b) 1975, c) 1998 and d) 2010. The Z error is represented by ellipse colour. The X, Y errors are represented by ellipses. The estimated GCP locations are shown with a dot or cross. (Red rectangle indicates the study area)

Table 3

The RMSE of residuals on GCP coordinates after the geo-registration [m]

Date	GCP #	RMSEX	RMSEY	RMSEZ	RMSEXY	RMSEXYZ
1951	6	1.54	1.60	1.86	2.22	2.90
1975	7	1.09	1.03	3.67	1.50	3.96
1998	7	0.80	1.30	2.52	1.53	2.94
2010	6	0.32	0.52	1.62	0.61	1.73

The RMSEs of the coordinate residuals on the GCPs were computed by Eq. (5) to (9):

(5)

RMSEX=∑(xs−xr)2n,

(6)

RMSEY=∑(ys−yr)2n,

(7)

RMSEZ=∑(zs−zr)2n,

(8)

RMSEXY=∑xs−xr2+∑ys−yr2n,

(9)

RMSEXYZ=∑(xs−xr)2+∑(ys−yr)2+∑(zs−zr)2n,

where subscript s is the surveying coordinates, and r is the estimated coordinates of GCPs. n is the number of GCPs.

Urban area change detection

The study was implemented on the common stereoscopic area of the 1951, 1975, 1998 and 2010 images (Figure 5). The created dense point clouds did not have a uniform grid, and they had holes due to the occlusion of buildings. Thus, dense point clouds were resampled as a uniform grid. The grid spaces were selected as 0.50 metres as the proper mean GSD of all point clouds.

The changes were estimated for the periods of 1951 to 1975, 1975 to 1998, 1998 to 2010 and 1951 to 2010. Of the two point clouds in each period, the oldest point cloud was selected as a reference, and the other (target) was registered into the reference coordinate system using ICP in PolyWorks software (Table 4). The changes were then estimated with distances computed from the points of the target point cloud to the mesh triangle of the reference point cloud (Figure 6, Figure 7).

Figure 6

The cross-section from compared data of 1951 and 2010. The height differences correspond to the changes.

Figure 7

The estimated changes (legend units: meters)

Table 4

The ICP convergence of compared point clouds

Date comparison	Convolution [m]	Mean [cm]	Std. Dev. [m]
1951–1975	9.2e-7	0.06	0.99
1975–1998	7.1e-7	-0.87	0.96
1998–2010	9.3e-7	0.09	0.94
1951–2010	9.1e-7	0.12	0.99

Analysis of the changes

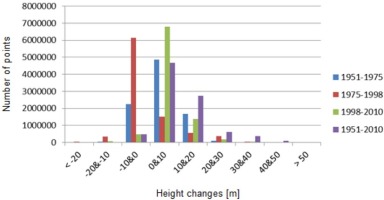
The sequential analysis of the changes showed urbanization and growth in the study area during the analysed periods. The RMSE of the estimated distances between two point clouds indicated the degree of change. The time intervals of the sequential periods 1951–1975, 1975–1998 and 1998–2010 are roughly similar, and their change degrees are also close to one another. For the period 1951–2010, because it is the longest period, its degree of change is greater than the others (Table 5).

Table 5

The change quantities for the historical periods

Year	RMSE [m]	Average d [m]	Std. dev. ᓂ [m]
1951–1975	8.42	4.82	6.91
1975–1998	8.51	-0.90	8.46
1998–2010	9.10	6.69	6.18
1951–2010	14.16	10.60	9.39

The distances between the point clouds were divided into 10 m intervals to compare the subinterval change degrees in all periods. The large change in the period 1951–1975 is approximately 10 m in the upward direction. There are many changes in the downward direction by approximately 10 m in height during the period 1975–1998. Average d in Table 5 also indicates the same inferences. These probably resulted from the

demolished adobe houses. New buildings generate change in the urban area. The changes related to the new buildings in the period 1998–2010 have a little more than the others. The comparison of the first epoch 1951 and the last epoch 2010 is shown an extensive 10–20 m change in the upward direction for all the study area. The higher buildings were constructed around 1998 in these periods, and some of them were reconstructed in places from which old buildings were removed (Figure 8).

Figure 8

The change comparison during the historical periods

6. Discussion

Current image-based measurement software is focused on automatic dense point cloud generation. Moreover, using a specific target shape, scale and geodetic registration can be attained for the model automatically. In this study, a dense point cloud was created from a set of uncalibrated camera stereoscopic images. The mean reprojection error smaller than one pixel shows the high accuracy of the photogrammetric evaluation.

The registration of the 3D point cloud model into the geo-reference system needs at least three GCPs in uniform distribution for high accuracy. Here, every 3D model was registered to the geodetic coordinate frame with six object-based GCPs. The establishment of object-based GCPs is very difficult, especially in open rural areas. Roads, rivers or fences can be used to define GCPs, but their error-prone selection from images leads to less accurate registration. Because the study area has many historical structures, statues, mosques, city arenas, it was possible to employ them to create the GCPs. An obstacle situation in the selection of the GCPs was encountered when measuring the geodetic coordinates with a GNSS receiver due to signal loss among high buildings. A new other detail was selected in this situation.

The point cloud density, which is 4–5 points/m², is sufficient to detect large-scale urban changes. The point cloud can include occlusion that occurs due to the shadow effect of buildings or less characteristic surfaces such as glass-covered buildings. Urban areas have a trivial number of less characteristic surfaces. Nevertheless, high buildings cause occlusion

in point clouds, which should be filled by interpolation from neighbouring points to correctly emphasize the changes.

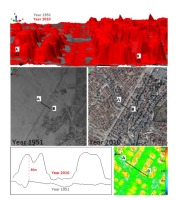
Urban changes were successfully measured using the proposed point-to-surface distances in this study. For example, an apartment building that was demolished in 2004 can be detected by a visual comparison between 1998 and 2010. Although the eleven-story building existed in 1998, it was not in the images from 2010. The comparison of these two point clouds showed a change in the downward direction (Figure 9). In contrast, two new eleven-story buildings west of the demolished building are shown by upward changes of approximately 35 m.

Figure 9

The changes due to demolished and new buildings from 1998 to 2010 (Unit: meter)

The comparison between 1951 and 2010 showed significant changes due to new constructions to the west of the railway. Although the region had any buildings in 1951, almost the whole side had new buildings according to the point cloud of 2010. The change process during this long historical period can be investigated via comparison with sequential small-period data (Figure 10). Whereas the comparison of point clouds between 1975 and 1998 indicated many new buildings, the comparison between 1998 and 2010 showed slow construction of new buildings.

Figure 10

The visualization of changes in comparison of time series point clouds (B1 location: 37°53’09.15”N latitude, 32°29’08.37”E longitude) (Legend unit: meter)

7. Conclusions

The dense point cloud method has been extensively used for surveying and 3D modelling in many applications. In this study, the urban changes between 1951–1975, 1975–1998, 1998–2010 and 1951–2010 were estimated by comparing two point clouds created from stereoscopic aerial images. After the target point cloud was registered to the reference point cloud by the ICP method, the changes between the two point clouds were estimated with point-to-triangle mesh distances. In addition, the changes in these four periods were analysed. The offered method allowed efficient detection of urban changes that had occurred as a result of the new constructions or destructions of buildings, extensions, excavation works and earth fill arising from urbanization or disasters. In addition, it enabled us to update the geo-databases, effective planning and disaster management. On the other hand, low cost imaging platforms such as unmanned aerial vehicles provide exploiting the method for strict control against the unauthorized activities.